Código fuente del proyecto: FdF
En uno de los proyectos de 42, se nos da una iniciación al mundo de los gráficos en 3D a través del proyecto FdF, las sigas de ‘fil de fer’ en francés, que significa wireframe model en inglés y modelo de estructura alámbrica en español.
En este proyecto se nos pide que a través de un archivo de texto y haciendo uso de la librería gráfica de la escuela, MLX42, leamos un mapa donde cada coordenada tiene el valor de su altura, y lo representemos gráficamente en 3D, con un formato como este:
$> cat 42.fdf
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 10 10 0 0 10 10 0 0 0 10 10 10 10 10 0 0 0
0 0 10 10 0 0 10 10 0 0 0 0 0 0 0 10 10 0 0
0 0 10 10 0 0 10 10 0 0 0 0 0 0 0 10 10 0 0
0 0 10 10 10 10 10 10 0 0 0 0 10 10 10 10 0 0 0
0 0 0 10 10 10 10 10 0 0 0 10 10 0 0 0 0 0 0
0 0 0 0 0 0 10 10 0 0 0 10 10 0 0 0 0 0 0
0 0 0 0 0 0 10 10 0 0 0 10 10 10 10 10 10 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Como preaviso, en 42 tenemos la Norma, varias reglas comunes para casi todos los proyectos, como por ejemplo que las funciones tienen que tener menos de 25 líneas y cada línea menos de 80 caracteres. Por este motivo, a veces he tenido que sacrificar la estructura o legibilidad del programa.
¿Qué es un wireframe?
Un wireframe es un algoritmo para renderizar objetos en 3D en el que solamente se dibujan las aristas de los vértices que componen el objeto modelado. Apenas requiere potencia de cálculo comparado con otros modelos de renderizado como el RayTracing, ya que no tiene en cuenta la luz ni utiliza ningún método para simular la visibilidad.
Ejemplo:

Arquitectura de la solución
Modelo de datos
En primer lugar, para poder representar puntos en 3D, necesitamos una estructura que contenga las coordenadas X, Y y Z de cada punto, además de su color. Para almacenar el color utilizaremos un entero sin signo de 32 bits, para poder almacenar 8 bits por cada color (r, g, b) y otros 8 para la transparencia.
typedef struct s_point
{
int x;
int y;
int z;
uint32_t color;
} t_point;
Ahora vamos con la estructura para el mapa. Necesitamos almacenar el resto de información, el conjunto de puntos 3D, el alto y ancho del mapa, y otros dos valores útiles como el menor y mayor valor de Z, que nos permitirán escalar el mapa para poder dibujarlo completo en la pantalla.
En un principio elegí representar los puntos como un array bidimensional, pero es mucho más rápido si lo hacemos en un array de una dimensión.1
typedef struct s_map
{
unsigned int width;
unsigned int height;
unsigned int len;
int min_z;
int max_z;
t_point *points;
} t_map;
Las estructuras anteriores nos servirán para determinar la posición del objeto en el mundo, pero si queremos verlo tenemos que crear una estructura para la cámara.
Aunque sea una estructura grande, en realidad su funcionamiento es bastante sencillo. Consideramos siempre que el objeto es el centro del mundo, y guardamos en offset_x y offset_y cuantas unidades tenemos que movernos en el eje X e Y para que al representar el objeto en 3D siga en el centro.
Con esto ya cumpliríamos los requisitos básicos pero he querido ir más allá e incluir varias mejoras. Utilizaremos z_scale para que los objetos con valores extremos de Z también se puedan ver bien en nuestro programa, y también he añadido los ángulos de cada eje y el zoom de la cámara para hacer que el programa sea dinámico y podamos recorrer el mundo.
typedef struct s_cam
{
int projection;
float zoom;
double z_scale;
int offset_x;
int offset_y;
double x_angle;
double y_angle;
double z_angle;
} t_cam;
Implementación de la solución
El funcionamiento del programa es el siguiente:
- Comprobar que se nos pasa un mapa válido.
- Guardar los valores de cada punto del fichero, convirtiendo de texto a número todos los valores y guardando los valores hexadecimales que corresponden al color.
- Inicializar la cámara.
- Inicializar la ventana del programa y la imagen donde vamos a ir pintando los puntos, utilizando la librería MLX42.
- Pintar en pantalla cada punto en el espacio 3D.
- Añadir un manejador de eventos que controle qué tecla se está pulsando y que transforme la imagen, ya sea moviéndola, haciendo zoom o rotándola.
- Liberar toda la memoria utilizada y cerrar el programa.
Vamos a profundizar en los puntos 5 y 6 ya que son los más interesantes, hasta ahora lo único que habíamos hecho es rellenar las estructuras que hemos explicado anteriormente.
Dibujando el mapa
Ahora que ya tenemos todos los datos listos, tenemos que empezar a pintar los píxeles en la pantalla.
Proyección de un punto 3D a 2D
En primer lugar tenemos la función que nos va a decir las coordenadas 2D de un punto que queremos representar en 3D. Esta función recibe una copia del punto que queremos proyectar y la cámara, y le aplica las rotaciones, el zoom, y hace los cálculos trigonométricos necesarios para representarlo en un plano isométrico.
He añadido varios comentarios a la función para detallar su funcionamiento.
t_point project_pt(t_point pt, t_fdf *fdf)
{
int x;
int y;
// escalamos posición x e y del punto a las dimensiones de la pantalla
pt.x = pt.x * fdf->cam->zoom - ((fdf->map->width * fdf->cam->zoom) / 2);
pt.y = pt.y * fdf->cam->zoom - ((fdf->map->height * fdf->cam->zoom) / 2);
// escalamos el eje z a la escala que hemos calculado tras recorrer el mapa
pt.z = pt.z * fdf->cam->zoom / fdf->cam->z_scale;
// rotamos el punto en los 3 ejes utilizando las matrices de transformación
rotate_x(&pt, fdf);
rotate_y(&pt, fdf);
rotate_z(&pt, fdf);
// aquí tenemos dos tipos de proyección, podemos verlo de forma isométrica y también desde un plano cenital
if (fdf->cam->projection == ISOMETRIC)
{
x = (pt.x - pt.y) * cos(ISO_ANGLE);
y = (-pt.z + (pt.x + pt.y)) * sin(ISO_ANGLE);
}
else
{
x = pt.x;
y = pt.y;
}
// colocamos el punto relativo al centro de la pantalla
pt.x = x + WIDTH / 2 + fdf->cam->offset_x;
pt.y = y + (HEIGHT + fdf->map->height) / 2 + fdf->cam->offset_y;
return (pt);
}
Algoritmo de Bresenham
Esta función no es todo lo legible que me gustaría, ya que tuve que descomponerla en varias funciones para pasar la Norma.
Una vez que ya tenemos el punto representado en el espacio 3D, aplicamos el algoritmo de Bresenham, que dibuja una línea de píxeles entre los puntos A y B.

Mi función es una implementación de este algoritmo, teniendo en cuenta además que el pixel que vaya a pintar esté en el rango de la pantalla para evitar renderizar una parte del mapa que no se muestra. Además, también he implementado una función que interpola linealmente los colores de los puntos A y B para crear degradados en las aristas.
Una vez que ya tenemos las coordenadas del pixel y el color, lo pintamos en la imagen con la función de la librería mlx_put_pixel.
void bresenham(t_point p0, t_point p1, mlx_image_t *img)
{
t_bresenham bres;
init_bresenham(p0, p1, &bres);
while (1)
{
if (p0.x == p1.x && p0.y == p1.y)
return ;
if (pixel_limits(&p0))
mlx_put_pixel(img, p0.x, p0.y, interpolate_color(p0, p1, bres));
if (2 * bres.error >= bres.dy)
{
if (p0.x == p1.x)
return ;
bres.error += bres.dy;
p0.x += bres.sx;
}
if (2 * bres.error <= bres.dx)
{
if (p0.y == p1.y)
return ;
bres.error += bres.dx;
p0.y += bres.sy;
}
}
}
Dibujar el mapa en pantalla
Ahora que ya tenemos las funciones que hacen todo el trabajo duro, lo único que tenemos que hacer es recorrer el mapa de puntos uniendo cada punto a sus vecinos. Si queremos dibujar el punto A(x, y), tenemos que pintar las líneas que lo unen al punto B(x + 1, y), y al punto C(x, y + 1).
Una vez que el algoritmo de Bresenham termina de dibujar la imagen, la añadimos a la pantalla con la función de la MLX mlx_image_to_window.
void draw_map(t_fdf *fdf)
{
unsigned int i;
unsigned int width;
t_point pt;
t_point *pts;
clear_background(fdf->img);
i = -1;
pts = fdf->map->points;
width = fdf->map->width;
while (++i < fdf->map->len)
{
pt = project_pt(fdf->map->points[i], fdf);
if (i % width != fdf->map->width - 1)
bresenham(pt, project_pt(pts[i + 1], fdf), fdf->img);
if (i + width < fdf->map->len)
bresenham(pt, project_pt(pts[i + width], fdf), fdf->img);
}
mlx_image_to_window(fdf->mlx, fdf->img, 0, 0);
}
Añadiendo hooks para que sea interactivo
La librería que nos dan para el proyecto tiene varias funciones para manejar eventos.
A través de la función mlx_key_down, podemos detectar qué teclas está presionando el usuario y determinar el comportamiento del programa. Este sería un ejemplo de un hook para controlar el movimiento de la cámara:
void movement_hook(void *param)
{
t_fdf *fdf;
fdf = param;
if (mlx_is_key_down(fdf->mlx, MLX_KEY_W))
fdf->cam->offset_y -= MOVE_SPEED;
else if (mlx_is_key_down(fdf->mlx, MLX_KEY_S))
fdf->cam->offset_y += MOVE_SPEED;
else if (mlx_is_key_down(fdf->mlx, MLX_KEY_A))
fdf->cam->offset_x -= MOVE_SPEED;
else if (mlx_is_key_down(fdf->mlx, MLX_KEY_D))
fdf->cam->offset_x += MOVE_SPEED;
else
return ;
draw_map(fdf);
}
En este caso, el programa detecta cuando se está pulsando las teclas WASD y mueve la imagen hacia arriba, izquierda, abajo, y derecha respectivamente. Una vez que ya tenemos la función creada, tenemos que añadirla al bucle principal con la función mlx_loop_hook. Su uso es el siguiente:
/* mlx_loop_hook(
instancia de MLX a la que añadir la función,
puntero a nuestra función,
parámetro que recibe la función
) */
mlx_loop_hook(fdf->mlx, &movement_hook, fdf);
Resultado final
Mapas
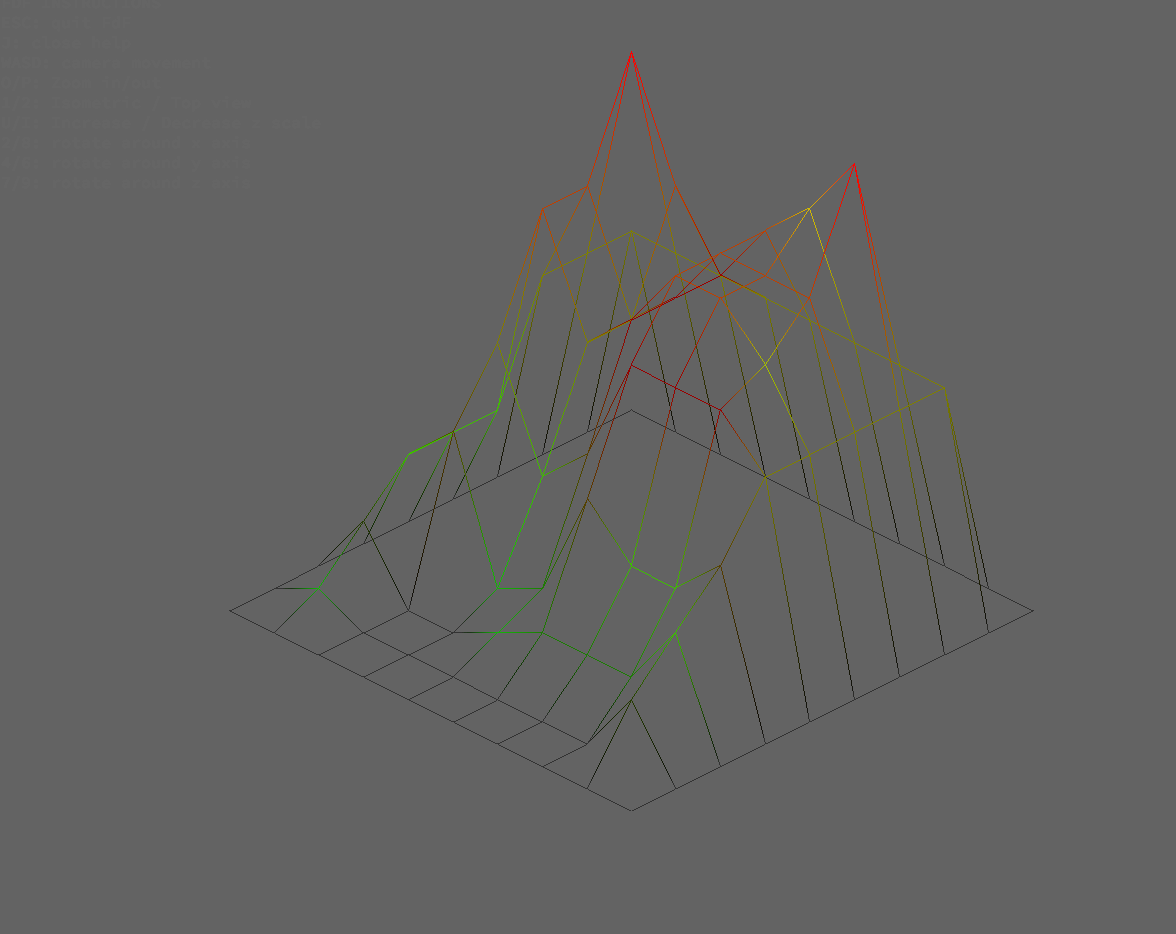

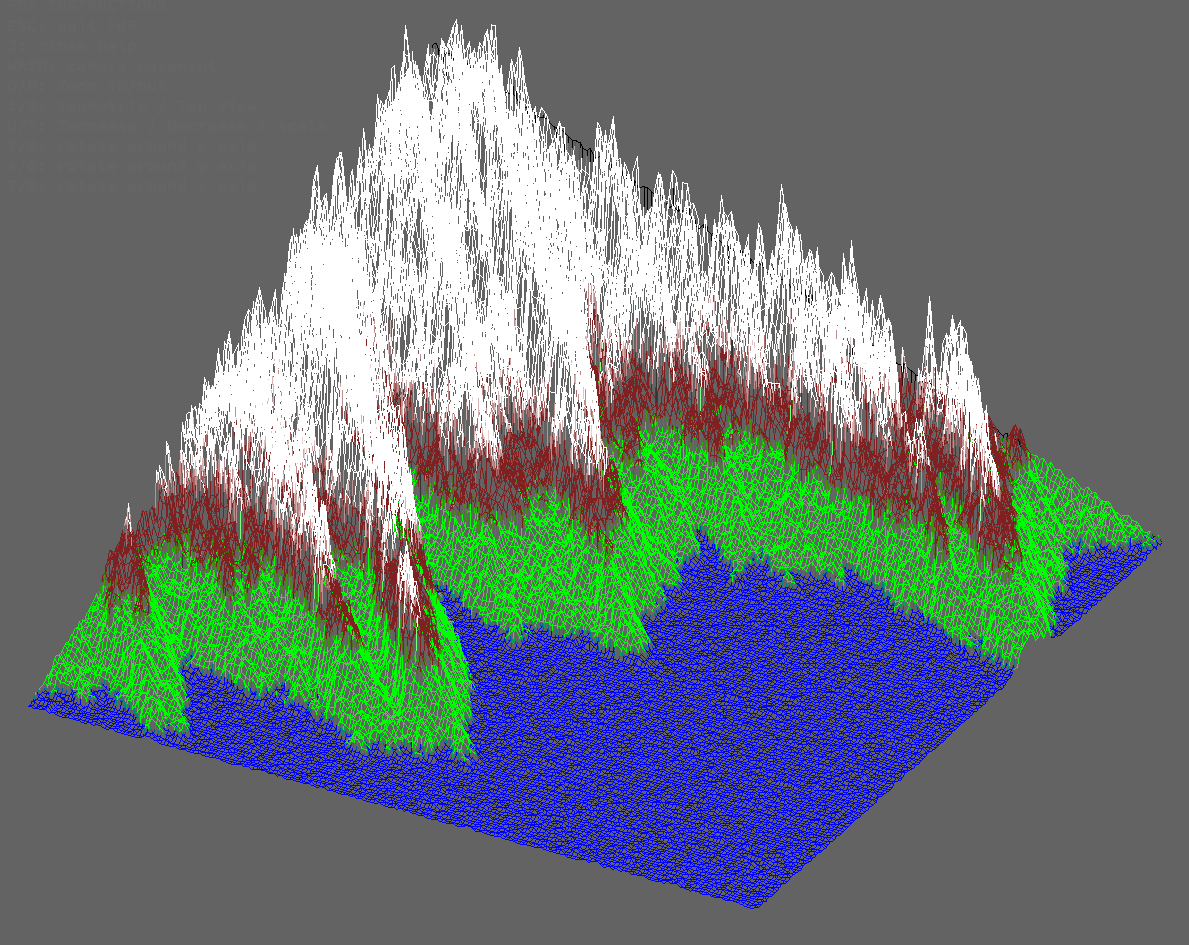

Zoom

Rotaciones

Movimiento

Ajustes en la escala de Z

Otros tipos de proyección

Bonus: modo arcoiris!

Conclusión
Ha sido un proyecto muy satisfactorio, la programación de gráficos es de las cosas más gratificantes que hay, ya vas viendo la evolución de tu programa según pasan los días, y pasas de pintar puntos individuales a imágenes completas.
También es más complicado de debuggear, ya que para renderizar una imagen de 1000x1000 píxeles se llama a la función bresenham más de 2 millones de veces, y al trabajar con números de coma flotante, a veces ocurren problemas que se escapan a nuestro control.
Ha sido una gran experiencia y por fin he utilizado la trigonometría que aprendí en cuarto de la ESO, sabía que este día llegaría!
